|
Like the title? Disregard it. It is a lie. It is about the
empirical design of propellers. Also it is really about how
Supercool discovered the late E. Eugene Larrabee, and came
to hate his equations for propeller analysis. “Analytic”
means you start off with nothing, throw in lots of equations,
and end up with something cool. Try reading a book on Fluid
Dynamics. Talk about fanciful. Those guys don’t even
get out of their armchairs. But I’m not sure that they
are at all cool.
An example: I need to understand how airfoil
“downwash” affects the “induced” angle
of attack. After reading a dozen authors, I’m none the
wiser. Some seem to say the opposite of the others. Some are
on the dark side of the moon.
Once again, Supercool has to invent his own
reality. Refer to “Analytic
Design of Propellers: Part3. Induced angle of attack”.
Another example: I have spent quite literally
a thousand hours over 20 years trying to get Larrabee’s
equations to design a realistic propeller for model aeroplanes,
and failed. It may well be that the induced angle-of-attack
problem mentioned above may have been my Nemesis. Despite
this, Larrabee remains my “Om mani padme hum”.
(Jewel in the Lotus).
After all this failure, where do we go from
here? Well, while writing a turbine code for my son, I was
struck by a rare insight. Very rare. All my life I have admired
the handful of genius’s who created modern Maths and
Physics: never have I had a new or original thought. But at
last I have at least had a derivative thought, and I plan
to milk it until it bleeds!
By way of background, my propellers are CNC
machined to aerodynamic known parameters of diameter, blade
angle, and airfoil. Further, from Doppler analysis I know
their performance in the air, by way of airspeed and RPM.
This is pretty neat: all I don’t know about them is
whether the design is optimal. Maybe a change in airfoil would
make them better, or a change in blade angle? But what new
value should I try? No idea. So some sort of theory is really
necessary.
Now back to the insight. What do we have? Well,
we’ve got a pretty good idea how fast the air is entering
the propeller disc from in front, because we know the airspeed.
We know how fast the air is entering the prop disc from the
side (well tangentially, anyway), because we know the RPM.
We also know the advance per revolution, sometimes called
the “effective pitch”.
But we also know the geometric pitch, because
we know the blade angle. The problem is, the effective pitch
is less than the geometric pitch by some strange amount. This
is due to the aforementioned “downwash”. If we
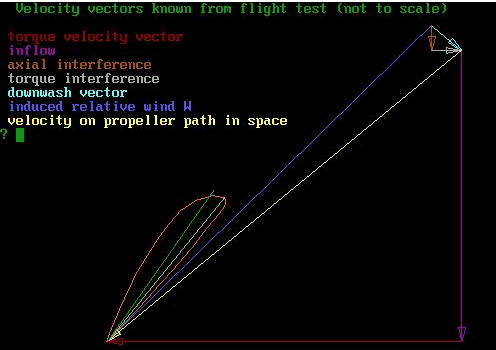
regard this “downwash” as an actual velocity of
the air, at right angles to the actual inflow to the airfoil,
then we complete a vector diagram of airflow components with
3 sides and a resultant.
Now this is incredibly cool. Because
the “interference factors” are just the axial
and torque components of the down wash, we know these factors
without using any fluid dynamics at all! You see; the prime
problem in propeller vortex theory is to determine these interference
factors. We know them already without lifting a finger!
All that is unknown to us is the angle the
airfoil is actually making with the inflow of air to the blade.
So we resort to an equation originating with Joukowski, which
lets us calculate the airfoil lift coefficient for our particular
flight condition.
Refer to “Analytic Design
of Propellers: Part2. Determination of c1”.
Well, it would if we knew the airfoil angle
of attack, and right now we don’t.
Suppose we guess a value of lift coefficient
which might apply to our airfoil, and call this the “design”
lift coefficient. This will vary along the blade due to compressibility,
but that is secondary to our discussion here.
We now have 2 lift coefficients, one for our
guessed angle of attack and one we want to have, as being
reasonable, like C1 = .5 for Clark Y.
This is not too good, we only want one value,
not two, and we want to know the angle of attack. Well, that
is OK. Lift coefficient and angle of attack are dependent
variables: know one, know the other. This relationship is
called the “lift slope”, and we have a pretty
good idea of what that is.
All we have to do is guess new
values for angle of attack until the Cl we got
from Joukowski is the same as the “design” Cl,
and we are done!
Yes folks, given that we already know the propeller design
and its performance, we can now predict its performance retrospectively!
How is that for a once-in-a-lifetime revelation! You are cool,
Supercool, very definitely!
Now what use can we make of all this? Can we
show that the design Cl is the right one? What
can we do to improve the propeller?
Well, we might want the propeller to have “minimum
induced loss”, whatever that is. Sounds good, so lets
have some of that. Well, we have “minimum induced loss”
when the axial component of the slipstream velocity (which
makes thrust) is uniform across the prop disc.
This point can be understood if we remember that thrust results
from the momentum change of the air passing through the prop
disc, this thrust being directly proportional to induced velocity.
By contrast, the energy required to produce this induced velocity
is proportional to the square of that velocity, so it comes
at some cost. If there is some annulus in the slipstream with
a higher induced velocity, then more energy is required, which
is thus disproportionate to the other annuli. On average over
the whole prop disc, more energy is required to produce the
same thrust, and hence efficiency is lost .
Returning to our problem: how can we make the
axial slipstream uniform over the prop disc? Our good friend
Joukowski again provides a clue. He reckons that the downwash
velocity depends on the blade chord. So all we have to do
is vary the blade chord from root tip until all the slipstream
annuli have the same induced axial velocity. As Biggles would
say: piece of cake!!
By now, our original prop design is lost in
the noise. We have a new prop design. Regrettably, it does
not match our original, as we would have hoped. Something
in our physical model of the propeller has gone astray. The
chord is wrong, the pitch is wrong, we have new blade angles.
There are important factors we have neglected.
However, we may use our method to find them.
Prime among these deviant factors is the axial
inflow to the propeller. The speed of the plane is not necessarily
the inflow velocity seen by the prop. The spinner, and the
presence of the fuselage/wing behind the propeller disc all
modify the axial inflow velocity. The net effect is to reduce
the axial inflow velocity, with the greatest reduction occurring
at the root and the least at the tip. This reduction may be
of the order of 20% at the root, dependent on configuration.
In our calculation, we must introduce this
variation to our vector diagram.
Since the prop needs less pitch to match the reduced inflow
velocity, our original calculation of pitch will have been
too high. Matching the blade angles in this way provides a
means of estimating the reduction in inflow velocity.
Care is needed, as there are other variables.
The change in lift with angle of attack (the lift slope) is
also important. Propellers nearly always end up running high
Mach numbers near the tips. In models, anything from .6 to
.9 is quite common. The effect of compressibility on the lift
slope cannot be ignored. Fortunately this change can be estimated
by using the Glauert-Prandtl rule, which is very useful for
our purposes.
The theoretical value of the lift slope is
0.1 per degree for thin airfoils. However, variations from
this value can be quite large, depending on the shape of the
airfoil section, in particular, the leading edge. Sharp leading
edges can give lift slopes of .12 or more for small angles
of attack.
The drag of the airfoil section depends on
the airfoil thickness and Mach number, although this is not
such a critical factor as the foregoing effects.
The airfoil section itself is tricky to choose.
There is not much in the way of high-Mach low-Reynolds number
data. The safest approach is to use the thinnest airfoils
your materials permit, especially at the tips. Also avoid
blunt leading edges. The NACA 4-digit sections tend to be
too blunt. I have had success modifying the upper surface
forward of x/c = .3 with a simple circular curve.
More interesting is a comment by Weick. He
experimented with circular sections, flat-bottomed model-sized
sections (24”) in the wing tunnel and found them to
be superior to conventional sections. This plus the whirling
arm test results of Suzuki lead me to try these sections,
and so far they have been very good!
Shock wave formation for M>.85 is a concern.
About all you can do is use thin, sharp, flat-bottomed airfoils
with the high point back past x/c = .5
The rest is technicalities. I attach the Quick
Basic source code, which is heavily commented. Good luck with
it!
|