|
You must congratulate me, for this is my most outrageous title
yet. In fact, is has little to do with transonic flow at all.
This time we are going to look at the pure subsonic flow problem,
below M = 0.7 . Well, why bother?
At the heart of propeller design is the question of how
much lift we can generate efficiently for each radial station
along the blade. As we have seen, the flow problem in the
transonic region is little short of catastrophic. Even if
the tips aren’t blowing air backwards, they can sure
be soaking up engine power without giving much in return.
Hence the need for special airfoil sections, which are little
documented in the lay aerodynamics press.
But even for subsonic flow, there are still problems. For
a start, try finding data for airfoils with low Reynolds number
and Mach numbers around 0.5. We can always assign a value
for the lift coefficient, but what about the zero-lift angle
of these airfoils? What we need are some rules for handling
the aerodynamics from M = 0 to M = .7. Luckily they exist
and are quite good enough, but first let’s have some
fun.
Here is a very fundamental formula for lift force, L:
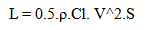
First note the mixture of Greek symbols with Roman. That
is a good tip-off. If it’s all in Greek characters,
the author is not confused: muddled, even wrong, but not confused.
If it’s all in Roman, he is uncultured. But mixed Greek
and Roman? I am now going to explain this formula to you exactly
as it is written.
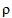 is
the air density. 0.5 is 0.5. Cl is a constant of proportionality
called the “lift-coefficient”. Note the violation
of the spelling rule “i before e except after c”.
Also, Cl is not a constant, but is in fact a function of Reynolds
and Mach numbers. What is more, if you look this number up
in tables, you will find that it applies to a wing of infinite
aspect ratio. We can live with that. V is the velocity of
the airplane with the assumption that air is incompressible.
In fact, air is highly compressible, but that is merely an
inconvenient truth. Finally, S is the area of the infinitely
long wing, so its value is the mean chord times infinity. is
the air density. 0.5 is 0.5. Cl is a constant of proportionality
called the “lift-coefficient”. Note the violation
of the spelling rule “i before e except after c”.
Also, Cl is not a constant, but is in fact a function of Reynolds
and Mach numbers. What is more, if you look this number up
in tables, you will find that it applies to a wing of infinite
aspect ratio. We can live with that. V is the velocity of
the airplane with the assumption that air is incompressible.
In fact, air is highly compressible, but that is merely an
inconvenient truth. Finally, S is the area of the infinitely
long wing, so its value is the mean chord times infinity.
So we have a nice, simple formula that is about as useful,
in the words of my master Andy Kerr, as tits on a bull. We
shall return to this quantity Cl after a brief word from our
sponsor.
I did mention a problem in finding the zero-lift angle ao
of a fully subsonic airfoil. Well it turns out that there
are some nice solutions to this problem based on thin airfoil
theory. Abbott and Von Doenhoff give methods on page 72 attributed
to Munk and separately to Pankhurst, which are quite adequate.
I don’t use them, because they give the same result
as a much simpler expression given by….I can’t
remember! But here it is anyway
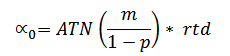
where
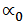 = zero lift angle in degrees
= zero lift angle in degrees
m = airfoil camber … typical value .0355
p = camber line high point … typical value .4
rtd= conversion factor radians to degrees [180/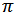 } }
ATN is the trigonometric operation arc tan
For these typical values, we get
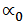 = -3.38 which is not too different from the value found in Soartech 8 at low Reynolds number for Clark Y.
= -3.38 which is not too different from the value found in Soartech 8 at low Reynolds number for Clark Y.
We are nearly ready to move on. Just one more thing. There
is a thing called the lift-slope. Bad English, so it must
be American. When you increase the angle of attack of an airfoil,
you get more lift. Surprisingly, for most thin airfoils, the
value of the lift-slope is pretty well constant. That value
is 0.09 degree^(-1). Good god, what?
Let’s try an example.
Choose an angle, say 5 degrees. Then the lift coefficient
increases by 5 * .09 = .45 Typically, for most reasonable
airfoils, the lift coefficient varies from -0.2 to 0.85. Above
0.85, the airfoil is getting close to the stall. Below –0.2,
we are looking at a cambered airfoil which is about to do
a negative stall!
So to review. We have a thing called lift-coefficient. Also
a thing called zero-lift angle and yet another thing called
lift-slope. If you have those things figured, we can move
on.
What we are looking for is the behaviour of the lift coefficient
as affected by Mach number. In figure 2 below, look at the
red and yellow curves for Mach number less than 0.7. Mach
numbers below 0.7 are generally “subsonic”. There
is no point on the airfoil where the local flow has exceeded
Mach 1. We are not dealing with the shock-waves which gave
us the horrors in the transonic region.
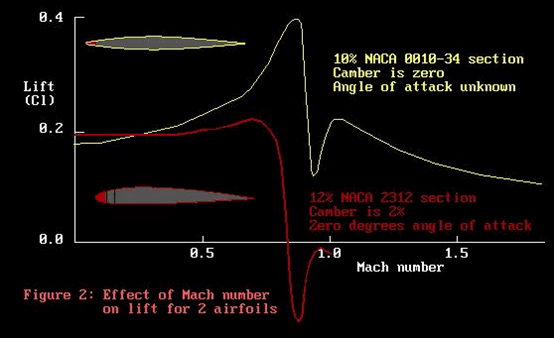
Both these airfoils show an increase in the lift coefficient
as the Mach number increases. There is a rather greater increase
for the yellow airfoil than the red, which is confounding.
For this exercise, we will pretend they are the same!
This increase in lift coefficient with Mach number is a compressibility
effect. There is a very simple formula which allows us to
calculate this increase in lift coefficient. The formula is
called by Milne-Thompson the “Glauert correction”,
and by other authors as the “Glauert-Prandtl rule”.
It is of great value to propeller designers, as virtually
every propeller has a strong radial change in Mach number
from root to tip. In F3D and F2A, this change ranges from
0 out to .95, which is really quite a problem.
If this rule lets us cover the subsonic region, then at least
we have that covered. But just what is this rule, and how
may it be applied? Well, first let me have a moan. For years
I have been aware of this rule, but being a simple soul I
could not see how to apply it. In my defence, let me quote
from some texts.
First off the rank is Godsey and Young, ”Gas Turbines
for Aircraft”, 1949. Try this for a mouthful.
“Consider a flow with free-stream Mach number Mo over
a thin airfoil of thickness t set at an angle
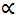 .
The drag and lift are affected by compressibility as if the
flow were an incompressible one for a similar airfoil having
thickness, not t, but t / .
The drag and lift are affected by compressibility as if the
flow were an incompressible one for a similar airfoil having
thickness, not t, but t / 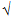 (1-Mo^2):
having angle of attack, not a, but (1-Mo^2):
having angle of attack, not a, but
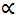 /
/ 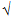 (1-Mo^2):
and having its camber increased in the ratio (1-Mo^2):
and having its camber increased in the ratio
1 / 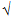 (1-Mo^2).” (1-Mo^2).”
I can still remember the first time I read this. I was on
the bus heading home from the reactor site. If only Nuclear
Physics were as clear as this. All I had to do was find data
for an airfoil stretched in 3 different directions and the
job was done. I don’t think!
Next off the rank is my old mate Milne-Thompson in “Theoretical
Aerodynamics”, who threw in a lot of mathematical chaff
with the oats. Try this:
“Case I. 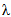 = 1,
v
= 1. Here the chords are equal but the camber and thickness
of A are those of Ai, reduced in the ratio ß:1. The
lift, circulation, and pressure are the same at corresponding
points in both flows. The incidence is reduced in the ratio
ß:1.
= 1,
v
= 1. Here the chords are equal but the camber and thickness
of A are those of Ai, reduced in the ratio ß:1. The
lift, circulation, and pressure are the same at corresponding
points in both flows. The incidence is reduced in the ratio
ß:1.
Case II.
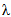 = 1/ß,
v
= 1. Now c =
ßci, so that the chord of A is less than
the chord of Ai in the ratio ß:1 and the camber and
thickness are reduced in the same ratio at corresponding points.
The lift, shape, incidence and circulation are unaltered;
the pressure is increased in the ratio 1:ß.
= 1/ß,
v
= 1. Now c =
ßci, so that the chord of A is less than
the chord of Ai in the ratio ß:1 and the camber and
thickness are reduced in the same ratio at corresponding points.
The lift, shape, incidence and circulation are unaltered;
the pressure is increased in the ratio 1:ß.
Case III. 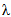 = 1, v
= ß. In this case ß/
v
= 1 and the distortions are the same in both flows. Thus A
and Ai are identical profiles at the same incidence. The circulation,
lift and pressure are increased in the ratio 1:ß. Thus
the effect of compressibility on a
given
profile is to increase the lift in the ratio 1:ß.
“
= 1, v
= ß. In this case ß/
v
= 1 and the distortions are the same in both flows. Thus A
and Ai are identical profiles at the same incidence. The circulation,
lift and pressure are increased in the ratio 1:ß. Thus
the effect of compressibility on a
given
profile is to increase the lift in the ratio 1:ß.
“
End quote. That very last line is the clue. No more bending
and twisting the airfoil profile. This is the same airfoil
we started with. Compressibility changes its lift. Good old
Milne-Thommo.
Perhaps I could have saved myself some trouble if I had
understood Abbott and Von Doenhoff’s conttribbution.
“The Glauert-Prandtl rule relates the lift coefficient
or slope of the lift curve of a wing section in compressible
flow with that for incompressible flow”.
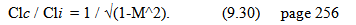
With c
meaning “compressible” and i
meaning “incompressible”, this works. But I still
can’t see how it works for the lift slope. Guess I’ll
just have to stay thin and ignorant. |