| You've backed up
for still more? I assume you have read Parts 1 and 2 as otherwise
this Part 3 will be incomprehensible. If not, here is a brief
reprise.
"So our fluid dynamics problem is to represent the
flow of air over a cliff or hill, on some sort of diagram.
This diagram will have lines on it, like contours, called
"streamlines": also, it will have a picture of a
cliff or hill. Think Stanwell Tops, Torrey Pines, or up past
General Cornpone on Mount Clarence.
We have a hill. It is outside of Esperance, in Western Australia,
which is one beautiful town, about as far from anywhere as
you'll ever get. It looks out over the Southern Ocean, so
wind-farms and slope soaring are “de rigeur”.
The wind coming off the Southern Ocean has travelled a few
thousand kilometres over water to get to our hill. So it is
pretty smooth, no turbulence from trees, just the occasional
wake turbulence from a passing Albatross or Cape Barren Goose,
or blast of hot air from Horace, the farting Sea Lion.
So now we get a definition. The path the wind follows is
a "streamline". The same air remains in the streamline,
but it can go faster: its pressure and density can change,
but it is still the same streamline, with the same air.
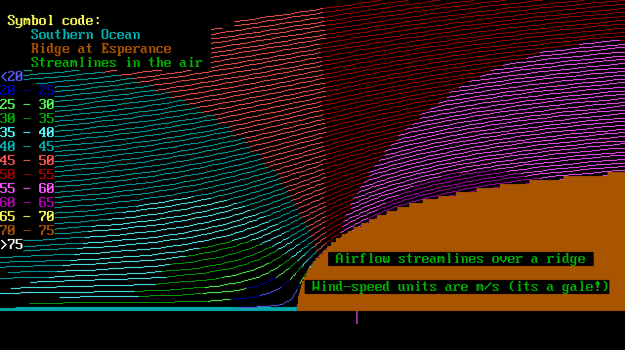
End reprise. So we have the streamlines, coming off the
sea and climbing over the ridge. We also have the speed of
the air as it runs along the streamlines. Now it would be
interesting to know the pressure distribution as well, but
how do we get it?
Fortunately Edward R. C. Miles, a research mathematician
at The Johns Hopkins University at Baltimore, USA, 1950, felt
the need to publish a book called “Supersonic Aerodynamics”.
On page 13 of this book he has the Saint-Venant and Wantzel
equation, which is a version of the Bernoulli Equation adapted
to adiabatic flow. The beauty of this equation is that it
relates pressure to velocity directly: ie, knowing velocity,
we can easily calculate the pressure.
For some mad reason he has it the other way around, ie, getting
velocity from pressure. In our work here, we have started
with the flow flux and derived the velocity in the streamlines:
I guess if you were measuring airspeed using a pitot tube
his equation would have made more sense.
I’ll see if I can trick MS Word into letting me write
this equation out.
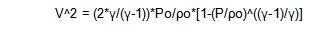
We have:
V = wind-speed, m/s
^ means raise to the power of
y = the ratio of specific heats at constant pressure and
constant temperature, which has the value of about 1.4.
y is the Greek letter “gamma”
Po = the pressure in the air when the wind is not blowing
po = the air density when the wind is not blowing: units
are Kg/m^3 = 1.28. That’s right, one cubic metre of
air weighs 1.28 Kg! ? is the Greek letter “rho”
P = the air pressure in the flowing air, MKS units are
Kg/m^2
Don’t worry about this maths too much, I have entered
the equation into my computer and we can see the result below.
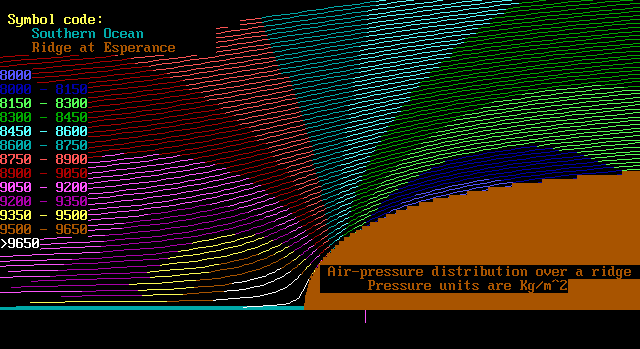
For the non-mathematically minded, here is a plot of the
streamlines, where the colours indicate the pressure bands
present in the streamlines. Look carefully and you will find
that the pressure at the bottom of the cliff is right up.
In fact, at the bottom of the cliff the wind has stopped.
This is called the "stagnation point".
This is just the opposite of the wind-speed. What we find
is that when the wind-speed is high, the air pressure is low.
Also of interest is the pressure at the maximum wind speed.
This occurs just a little back from the brow of the ridge.
At that point, the pressure is at a minimum. Right where you
want to stand while piloting your slope soarer!
|