|
You've backed up for more? I assume you have read Part 1,
otherwise this Part 2 will be incomprehensible. If not, here
is a brief reprise.
"So our fluid dynamics problem is to represent the flow
of air over a cliff or hill, on some sort of diagram. This
diagram will have lines on it, like contours, called "streamlines":
also, it will have a picture of a cliff or hill. Think Stanwell
Tops, Torrey Pines, or up past General Cornpone on Mount Clarence.

Click to enlarge
In the photo above we have a hill. It is outside of Esperance,
in Western Australia, which is one beautiful town, about as
far from anywhere as you'll ever get. It looks out over the
Southern Ocean, so windfarms and slope soaring are de rigeur.

Click to enlarge
The wind coming off the Southern Ocean has travelled a few
thousand kilometres over water to get to our hill. So it is
pretty smooth, no turbulence from trees, just the occasional
wake turbulence from a passing Albatross or Cape Barren Goose,
or blast of hot air from Horace, the farting Sea Lion.
So now we get a definition. The path the wind follows is
a "streamline". The same air remains in the streamline,
but it can go faster: even its pressure and density can change,
but it is still the same streamline, with the same air.
This where we really start to get an idea of what fluid dynamics
is really all about. To get a representation of the granite
ridge, we need to replace the granite ridge by some sort of
flow (in metres per second). This new type of flow, called
a "source", we will combine with the wind heading
toward the ridge. Sounds weird, but there you go. Nobody said
fluid dynamics was not weird!
In the maths, we are going to use this "source"
to deflect the uniform stream coming off the Southern Ocean,
thereby having the effect of our ridge."
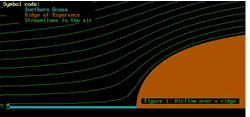
Click to enlarge
End reprise. So we have the streamlines, coming off the sea
and climbing over the ridge. What we don't have is the speed
of the air as it runs along the streamlines. Now that would
be interesting to know, but how do we get it?
Well, it turns out that the speed component in the direction
parallel to the sea, u, the x-component, is the rate of change
of flux in the height (y) direction. Similarly for the y component,
v,which is given by the rate of change of flux in the x direction
(sea). The sum in quadrature of these components is the speed
along the streamline.
Then we have:
u = U + m * x / (x^2 + y^2)
andv = m * y / (x^2 + y^2)
For the mathematically minded, these are the partial derivatives
of the total flux E, derived in Part 1.

Click to enlarge
For the non-mathematically minded, here is a plot of the
streamlines, where the colors indicate the speed bands present
in the streamlines.
Look carefully and you will find that the speed at the bottom
of the cliff is right down. In fact, at the bottom of the
cliff the wind has stopped. This is called the "stagnation
point". It is a good place to have your picnic, but beware;
there are 2 problems with that.
Problem 1: the tide must be out
Problem 2: Horace the Sea Lion likes that spot as well, and
if you think ants are a problem, then you just haven't lived!
Also of interest in the maximum wind speed. This occurs just
a little back from the brow of the ridge. Right where you
want to stand while piloting your slope soarer! Also a somewhat
inconvenient place. But if you think that is bad, try the
summit Mt. Clarence in Albany, WA. The lift is awesome, but
the landing zone is strewn with 3m high granite boulders.
Still, 3 hours of flying followed by an evening rebuilding
is a fair trade, especially since you are far away from farting
Horace.
|