|
Ever walked into a second-hand bookshop and found a classic?
It has happened to me 3 times. The first time I found Clive
Irvings "Wide-body: the triumph of the 747": I couldn't
put it down. The second time was a bookshop in Eureka, California,
called, unsurprisingly, Eureka Books, at 426 Second St. This
time it was the Den Hartog classic "Mechanical Vibrations",
from 1940. Great stuff.
The most recent time was at "Mainly Books", in
Bulwer Street, Perth. This treasure house was run by a couple
in their 80's. I knew it was "different" when I
first walked in. She was asleep at the till, bless her heart.
He was bolt upright in front of the computer, which was displaying
a blue screen saying "Error 404". He also was asleep.
So I tiptoed around to see if they had any engineering books.
And they did!

Click to enlarge
On the shelf was L.M.Milne-Thomson's "Theoretical Hydrodynamics"
from 1938. On the cover was the promise of "a thorough,
clear and methodical introductory exposition of the mathematical
theory of fluid motion, which will be useful in applications
to both hydrodynamics and aerodynamics". Right, that
seems good to me: after all, I have a double major in Physics
and Pure Mathematics, albeit gained 43 years ago. Still, with
my ego, the lapse of time and brain power should not be a
problem.
So I started reading each night when I went to bed. Then
I found why the old folks in the bookshop were so drowsy!
650 pages of vector algebra and complex variables: this is
not my idea of fun. So I skipped past everything that looked
hard, finding some goodies in Chapter 8. Now that would have
been OK if the book had a symbol table in the front (or even
in the back), but it did not. Evidently I was supposed to
know the symbols and theory from studying the preceding chapters!
Hells bells, how unfair is that!
Let me explain that. During my tender years at high school,
I liked to spend my time in the classroom designing contol-line
models. This meant hearing the teacher, but not listening:
in other words, inattention. Now the sadist teachers, and
they all were, did not like students with this propensity.
Their solution was a trick question, followed soon after by
a swish and a World Of Pain (WOP) which made sitting uncomfortable.
Now the trick question was this: "Sherlock, are you
listening?" The problem is that there are only 2 answers
to this. The first, and truthful one, was "no".
Not acceptable, swish, WOP. The second was to lie, "yes".
Now it was dangerous to lie, because the next question was
"what did I just say?". You see the "catch
22" situation, because if you did not know, swish,WOP.
Fortunately, we men have a divided brain, one lobe for lying,
the other lobe for telling the truth. I discovered that I
could train my lying side to remember only the last 3 words
that the teacher spoke. Now when he hit me with the "catch
22", I could tell him the last 3 words of whatever distraction
he was trying to make to my model designing. This seemed always
to satisfy his sadistic streak, thereby avoiding my making
a masochistic reply. This technique is known by pyschocolatists
as "Instantaneous Spontanteous Recall".
This early training had future implications. I found that
the important part of a novel was finding "who dunnit".
Now that fact was always revealed on the last page. To me,
being a Christian, it is the destination that matters, not
the journey: all I had to do was turn straight from the cover
page to the last page, thereby avoiding a lot of time wasting
rubbish in the intervening pages. Very efficient, if I do
say so myself, and it certainly took the tedium out of reading
Tim Winton's works.
Further on into the future, I found myself attending a series
of 20 lectures on General Relativity, a theory for which Albert
Einstein is well regarded by most informed dilettantes. The
last lecture ended with the presentation of the Energy-Momentum
matrix. This just blew me away, the whole universe neatly
summed up in one equation. That's the way to do Physics alright!
But why waste time with the intervening 19 lectures? Why not
just give the last lecture first? Then we could all go home
and build control-line models, much more fun.
It is not as though the lecturer knew what he was talking
about. There were quantities involved which were called "tensors",
which are sort of like complicated vectors. They came in 2
types, "covariant" and "contravariant".
This had me puzzled, so I did some reading in the Maths/Physics
library, eventually finding an author who stooped to actually
saying what they were. So far so good. Looking for positive
reinforcement, I ran this knowledge past the lecturer. To
my horror and amazement, he didn't know what I was talking
about!
Now regretably I find nearly all Fluid Dynamics books are
like this situation above. Lots of maths, but no explanation
at all of the physical concepts. Their treatment of Bernoulli's
equation is invariably incomprehensible. Since I wanted to
program the neat bit of maths on page 202, Chapter 8, I was
soon floundering, like Christian, in the slough of despond.
You know, the best quote from Milton is "Abandon hope
all ye who enter here". I think he was trying to read
up on Medieval fluid dynamics when he wrote that: it sure
is apposite.
OK. Now I have to practise what I preach. Or else be proclaimed
a hypocrite, or, worse still, an egregious hypocrite. This
means I have to give an explanation of a fluid dynamics problem
in words that you, my only reader, can understand! If you
are the sort of guy/gal who can watch steam pushing up the
lid of your cooking pot and then use this to design a steam
powered locomotive, we will get on just fine.
Here is what M-T (Milne-Thomson) has to say on page 203.
I quote "We can also regard this picture as representing
the flow of wind meeting a cliff". Gasp. You mean a slope
soaring site!! Now we are cooking with gas! Good old M-T would
have flown R/C slope
soarers, given the chance! Like being born 50 years later!
This I gotta play with.
So our fluid dynamics problem is to represent the flow of
air over a cliff or hill, on some sort of diagram. This diagram
will have lines on it, like contours, called "streamlines":
also, it will have a picture of a cliff or hill. Think Stanwell
Tops, Torrey Pines, or up past General Cornpone on Mount Clarence.

Click to enlarge
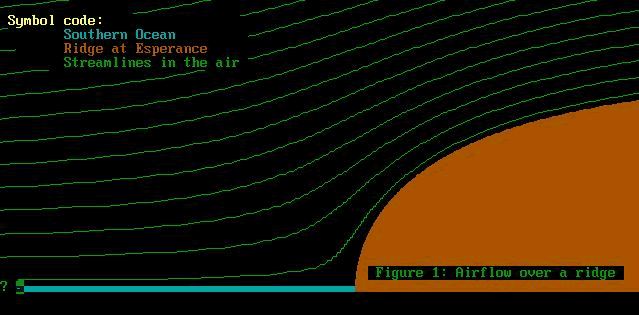
In the photo above we have a hill. It is outside
of Esperance, in Western Australia, which is one beautiful
town, about as far from anywhere as you'll ever get. It looks
out over the Southern Ocean, so windfarms and slope soaring
are de rigeur.

Click to enlarge
The wind coming off the Southern Ocean has travelled a few
thousand kilometres over water to get to our hill. So it is
pretty smooth, no turbulence from trees, just the occasional
wake turbulence from a passing Albatross or Cape Barren Goose,
or blast of hot air from a farting Sea Lion. In case you are
wondering where all this is, look in your Atlas for the Recherche
Archipelago (don't these French explorers have strange surnames?).
Now there is a worrying problem with air. Most times you
can't see it. But there are exceptions. One time I was trekking
thru the Cradle Mountain - Lake St. Clair National Park in
Tasmania, watching the weather carefully as you never know
when a blizzard will strike. Well, we were settling in for
the evening at Lake Windemere when I noticed a cloud running
along the top of a nearby ridge. To my amazement and delight,
the cloud did a right angle turn and came running down the
ridge slope toward the hut! Yikes, here were all these happy
campers lolling in the sun, completelty unaware of this novel
event. Hmm, this air could be cold, otherwise it would not
be pouring down the slope.
Quickly I slipped into my cold weather gear, and not a moment
too soon, as the ice cold air swept over the hut. Nobody was
hurt, but it was fun watching my fellow hikers hunting for
some warm clothes: especially the guy who had 3 girlfriends
in tow!
So now we get a definition. The path the cloud followed
was a "streamline". The cloud got faster as it went
down the ridge, but that happens with streamlines. The same
air remains in the streamline, but it can go faster: even
its pressure and density can change, but it is still the same
streamline, with the same air.
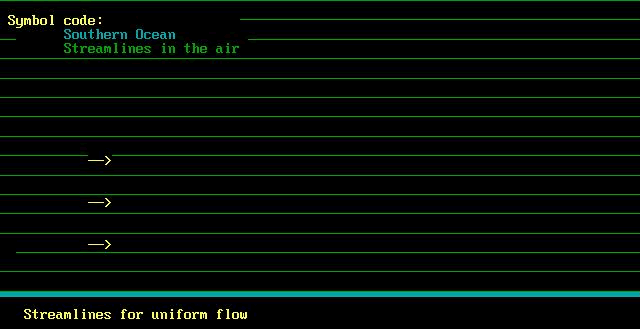
The figure above shows streamlines running over the sea.
The air has crossed over the sea and is flowing nice and smoothly:
what is more, the speed of the air is the same everywhere,
right up above the level of the ridge. In fluid dynamics,
this type of flow is called a "uniform stream".
Sometimes in aerodynamics it's called the "free stream",
but then it's not down by the sea: it's just in front of an
airplane which is going to disturb it somewhat, especially
if the airplane is a Tupolev 95 which has something like 30-odd
thrashing propeller blades!
Now the language of physics is mathematics, so we are going
to need some symbols and equations. Don't be put off by these
equations: if you can multiply 2 numbers together, then you
can do this! Just remember this; each symbol is just one number.
Here are the symbols:
U = speed of the uniform stream. Thats not so bad, now is
it? U just is a number like, say, 20. But because its a speed,
we have to say something like "U is 20 kilometres per
hour", or "U is 5.56 metres per second" (which
it is!). Instead of "is", we write "equals":
same thing.
y = height above the water (Southern Ocean, wherever). This
can be another number, say 60 metres.
Then we can write
E = U * y where the symbol E is the flux. Yikes, the flux??
What is that?
Imagine that the wall of air coming at us is only 1 metre
wide. Then the quantity of flux "E" is the volume
of air passing any given location at U metres/sec, y metres
high and 1 metre across. It is E cubic metres of air per second
going by. Returning to our previous
numerical examples, U is 5.56 metres/second and y is 60 metres.
The flux E is thus 5.56 times 60 which is 333.6 cubic metres
every second.
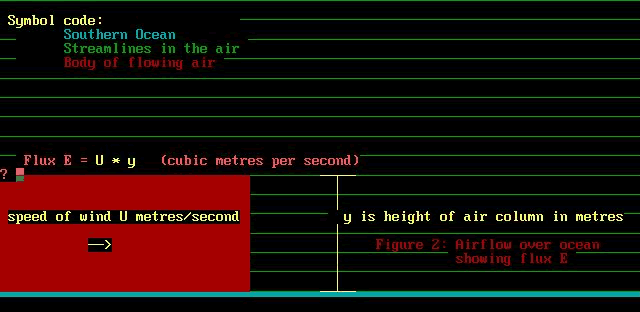
Now air is quite heavy stuff. One cubic metre of air at
sea level weighs 1.28 Kilograms! You wouldn't want a lump
of lead weighing that much to fall on your foot, that's for
sure! Now in our example, we have 333.6 cubic metres going
by, which has a mass of 333.6 * 1.28 which is 427 Kilograms.
That is nearly half a tonne! No wonder slope soarers and hang
glider guys get a blast from the rising air over a ridge!
Well so far so good. We have a mathematical expression for
the uniform stream of air approaching the ridge. Now all we
need is to get an expression for the ridge and we are well
on the way. But there is a problem. Our expression E for the
uniform stream is a measure of flow, in cubic metres per second.
The ridge is a big lump of granite, I guess measured in tonnes.
How are we to combine 2 such poorly matched quantities to
get the flow pattern of air over the ridge?
This where we really start to get an idea of what fluid
dynamics is really all about. To get a representation of the
granite ridge, we need to replace the granite ridge by some
sort of flow (in metres per second). This new type of flow
we will combine with the wind heading toward the ridge. Sounds
weird, by there you go. Nobody said fluid dynamics was not
weird!
This new type of flow is called a "source". Air
is considered to spray out into space from a central nozzle,
so that the air spreads out uniformly in all directions, much
like the blades of a fan. Also like the spokes in a bicycle
wheel. In case this still isn't clear, they say a picture
is worth a thousand words. Well here are 3000, Wordsworth.
Hand belongs to Rosie.
Other than that, the pictures show water being squirted
between 2 circular perspex plates. The water is deflected
(roughly) into a sheet spraying out into a fan. This is what
we mean by a "source" in 2 dimensions.



Click to enlarge
In the maths, we are going to use this "source"
to deflect the uniform stream coming off the Southern Ocean,
thereby having the effect of our ridge. Here is what it looks
like as a diagram.

We need a math expression for the source, just as we did
for the unifrom stream. Here it is, folks
S = m * t
S stands for the flux due to the source. Recall that flux
is the volume flow per second. ie, cubic metres per second,
just the same as for the uniform stream.
m has a special name, it is the "source strength".
Recall from the photos that water was being injected into
the centre of the source, then being deflected into the fan.
Well, that water flow from the tap is just the same thing,
the "strength" of the source. Just as for the
uniform stream, we take the width of the source to be just
1 metre. Then m is the flow per second per unit angle.
t is the angle in radians into which we are examining the
source. This calls for another diagram.
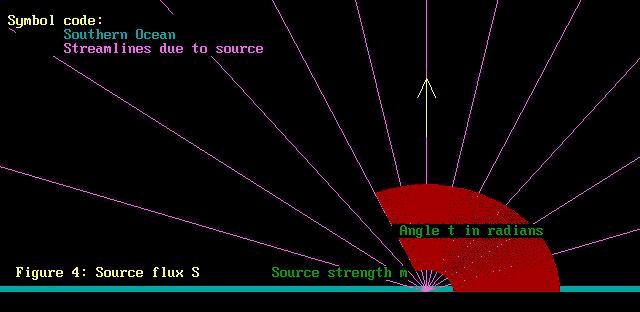
Having t as an angle in radians in the expression for S
is a bit odd at first sight. However, recall that the circumference
of a circle is 2 * pi * r where r is the circle radius and
2*pi radians is just 360 degrees. So multiplying by 2 * pi
is just multiplying be an angle!
Time to take a break. What have we achieved? Well, we have
expressions for the flux over the ocean and from an imaginary
thing called a source, probably located near to or inside
of the ridge. Now for the trick. I mean, here comes some real
fluid dynamics!
At any point in the flow, we are going to add the fluxes.
Then by taking lots of points, we are going to draw the streamlines!
Thus if we add E and S, we are going to get the flux anywhere
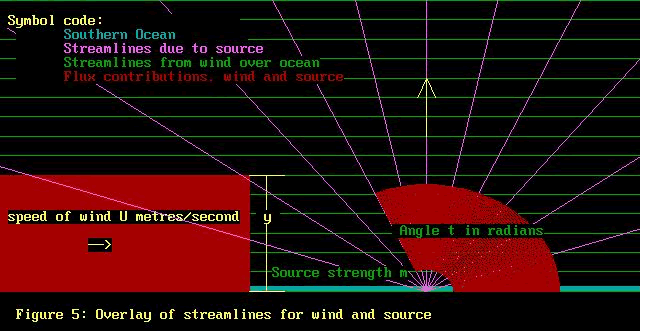
we want! Figure 5 shows everything we have done so far. Now
it remains to actually add the fluxes and thereby reveal both
the wind over the cliff AND the cliff!!
Thus Total flux F at any point = E + S
Now for an esoteric reason I don't really get, but which
is demanded by a convention in fluid dynamics, we are going
to assign negative values to these 2 fluxes E and S. That
is to indicate the flow is from left to right across the page.
A positive sign would indicate flow from right to left.
Now we have F = -E - S
= -U * y - m * t
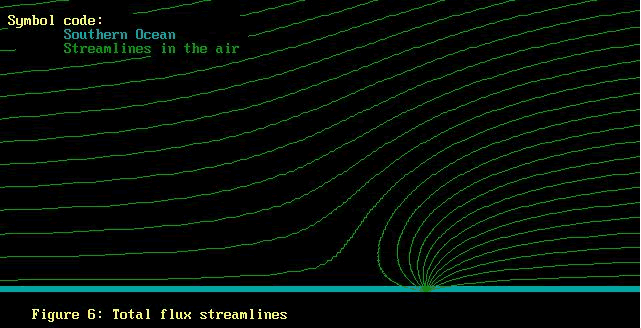
The result of adding the fluxes are the streamlines shown
in figure 6. To download the computer code which generated
these lines click here
(the format is .bas and is only 4kb). Wait a minute. How on
earth did the flow fields in Figure 5 ever yield the streamlines
in Figure 6? How did laying the source field on top of the
uniform flow field ever add up to get these curly streamlines?
Now this is true. I was laying in bed at 3:30 AM when the
answer to this question came to me. Luckily, I was not awake,
for then I would never have figured it out. The human brain
works in mysterious ways!
There is something Milne-Thomson failed to mention. Probably
because he knew it already, not realising we did not! It is
this. We cannot lay the flow fields on top of each other and
add them. To do so would imply that the fields mix. In other
words, the air from the source DOES NOT mix with the air from
the uniform stream. That is a little surprising. Rather, it
maintains its identity as air from the source. Same thing
for the uniform stream.
Here is another way of looking at it. The streamlines for
the uniform flow do not cross the streamlines from the source
field. Eureka! Now, just in case that remains as clear as
mud, maybe we need some diagrams.
Let us start with the uniform flow field, and add the source
flow starting with just a little strength and growing. Maybe
this will help. Note that the colours used for the 2 lots
of streamlines are different.
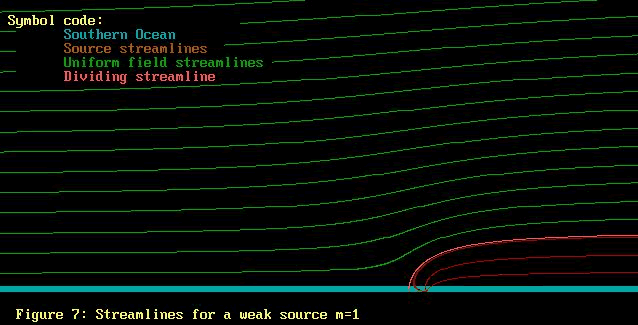
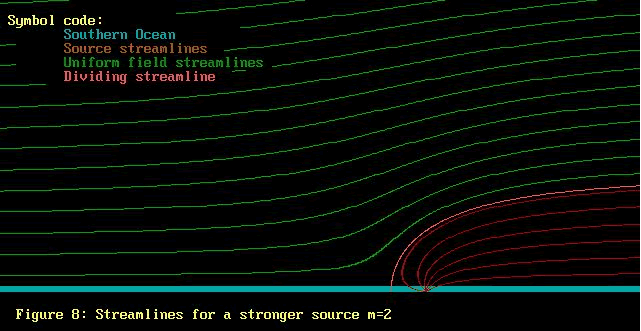
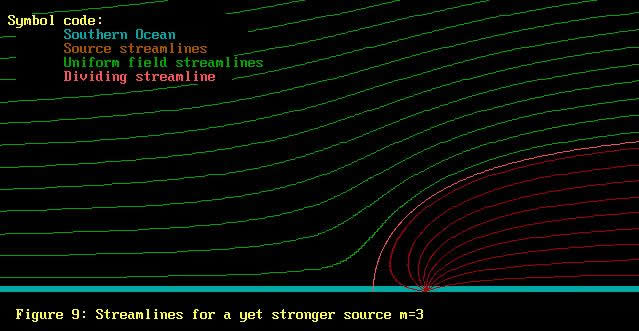
Hopefully it is now apparent from Figures 7 thru 10 that
the uniform flow field washes over the source field, displacing
the source field streamlines to the side. As the source field
strength grows, so the the source streamlines push further
up into the uniform field. The streamlines for both uniform
field and source field retain their identities, but become
distorted.
Now, dear reader, we are nearly done. Only 2 things left
to say.
Firstly, Figures 7 thru 11 have on them an extra streamline,
called the "dividing streamline". On one side of
this line is the air from the uniform field, while on the
other side is the air from the source field .
Finally, and this is the "piece de resistance",
there is no reason why the source field has to be air. It
only has to be a fluid. Lets make it molten rock, then cool
it to a solid so that we have a ridge of granite! Happy slope
soaring! But do wait for it to cool!

Thank you, dear reader for staying with me this far. There
is a lesson to be learnt here for authors. If you are trying
to explain something in print, then if you didn't understand
if before you started writing, you may well understand it
by the time you finish!
|