| All this transonic
flow stuff gets a bit confusing at times. When that confusion
happens, it is best to carefully dot the t’s and cross
the i’s, else, before you know it, you have answers
to questions you don’t even know about. Which just means
you haven’t understood what’s going on. At least,
that is how it works for me.
Being the author of this series, I have the right to fudge
and dissemble. That is exactly what I did in the previous
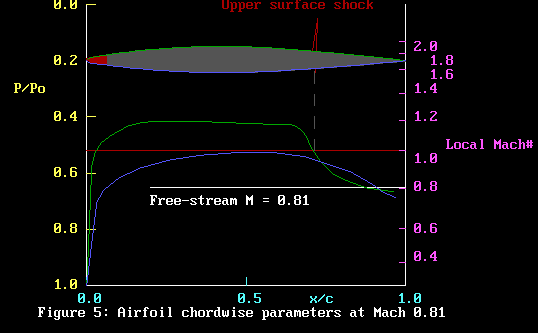
discussion. Remember that graph with no less than 2 vertical
axes? One was pressure ratio P/Po and the other “Local
Mach#”: at the time, I said that because you can draw
2 vertical axes, the 2 quantities involved must be related.
Well, that was true then, as it is now. However, I did not
have a clue why! Like I say, an answer with no question.
Recall that the pressure ratio P/Po is the ratio of the local
surface pressure P to the stagnation pressure of the air stuck
at the leading edge, the air there not knowing which way to
flow, over or under! Thus low values of P/Po represent “suction”.
Below is that figure again. Forget the shock stuff, we are
only looking at the vertical axes (ordinates) this time. At
“Local Mach#” of 1.0, I had drawn a red line across
to a value of P/Po slightly above 0.5. I really did that just
to show more clearly where the surface flow velocity went
supersonic. At the time, I wondered about this point P/Po
being near 0.5. Why on earth did it hit the axis at just that
point: not just there, but in all the figures, irrespective
of free-stream Mach number. Gotta be something weird going
there. And there is!
We need to look again at just what is meant by Mach #.
Well, its starts off nice and simple. Call Mach # “M”,
call the speed of the airplane “V” an the speed
of sound “c”, then:
M = V/c
How simple is that? Would you believe that in my book, “Propeller
Dynamics”, self-published in 1994, that I got that upside
down? My excuse is that I was dying at the time, so I was
in rather a hurry to build my pyramid. But then daughter Remy
saved my life, and here I am still writing this bumpf.
OK. Now I said this was simple, or even obvious. Since I am
usually lying when I say “simple” or “obvious”,
regular readers will know that the game is afoot!
Return to that great period of really bad fighter designs,
World War 2. Sir Sydney Camm of Hawkers produced a real monster
of a fighter, the Typhoon. Starting life with a massive 24-cylinder
RR Vulture engine, then progressing to the equally massive
Napier Sabre, also of 24 cylinders, the Typhoon made the Spitfire
look like a toy. But it had a serious problem (more than one
actually, but only one of relevance here). The wing was 18%
thick. That is good for keeping down the wing weight, or storing
big cannons and shells, but lousy for flying at high altitude!
You see, with more than 2000 HP up front, this aircraft was
intended to go fast. It didn’t. The problem was our
old friend, shock waves, resulting from high local Mach numbers
over that great thick wing. This problem was not so severe
at low altitudes, which meant the Typhoon was great for hedge-hopping
and firing rockets at tanks. But at high altitude in a dive,
the machine wanted to keep on going straight down, or even
tuck-under, despite the poor frightened pilot’s attempts
to pull back on the stick. If he had the courage to ride the
plane down to lower altitudes, then slowly the elevator would
start responding in the normal way. Recovery into level flight
then occurred (assuming (1) that the tail hadn’t fallen
off and (2), that he wasn’t holding full back stick,
in which case the wings ripped off)
This disconcerting problem suggests that at a lower, warmer
altitude, the shock wave problem went away. You see, the speed
of sound varies with temperature. It is cold at high altitudes
(like -40, Centigrade or Fahrenheit, take your pick),
so the speed of sound is much slower at 30000’ than
at 10000’. That is to say, Mach number varies with height,
simply because the speed of sound has changed.
So that is our first complication arising with our Mach number
formula. We need to consider temperature of the air. But it
gets worse. The speed of sound in air is also affected by
pressure and density. Since we have seen that pressure is
also affected by the speed of the air, it would seem that
the speed of sound, instead of being a nice steady 340 m/s,
can actually vary enough to upset the way an airplane flies.
Or even worse, it can upset our beloved propeller tips when
they go transonic. But before I move on, a little irrelevancy.
The quantities temperature, pressure and density are fundamental
to the study of air. They are called “state variables”.
The study of air involving these “state variables”
comes under the heading of “thermodynamics”. If
you think we are in a muddle already with shock waves, just
try following some thermodynamic analyses!
OK, now what is it that we were supposed to be working on?
Oh yes, the 2 vertical axes and the weird value of P/Po near
0.5 in our pressure diagram above. Consider that axis labelled
“Local Mach#”. Whitford really meant that. He
didn’t mean the speed of the airplane: he meant the
speed of the air flowing locally over the surface of the wing.
In our diagram above, that speed is considerably above the
free-stream Mach number of unity.
So here is a problem. The speed of sound in the air rushing
over the airfoil surface is affected by the speed of the air,
which has lowered the pressure of the air. Where does that
leave our definition of Mach#?. Well, we need a new one. Let
us say that “Local Mach#” is written M*, and the
speed of sound in air at the surface of the airfoil is c*.
Then:
M* = V / c*
When M* is less than unity, we say that the flow is subsonic.
When M* is greater than unity, we say that the flow is supersonic
Remember, M* is the local Mach#, which is to say, the Mach
number of the air rushing over the airfoil surface. We want
that, for the pressure drop it causes produces lift. But we
will come back to that later.
Now we don’t know the value of c*, but it turns out
that we don’t have to. Thanks be to Edward R. C. Miles
and his excellent book “Supersonic Aerodynamics”,
1950, all the messy thermodynamic reasoning has been done
for us. I quote from page 19.
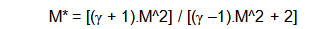
And
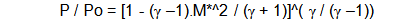
Recall that 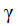 has
the value 1.4, being the ratio of specific heats at constant
pressure and at constant volume. That is the thermodynamic
stuff I was talking about earlier. It has to be a really neat
theory, because c* has disappeared altogether! has
the value 1.4, being the ratio of specific heats at constant
pressure and at constant volume. That is the thermodynamic
stuff I was talking about earlier. It has to be a really neat
theory, because c* has disappeared altogether!
Now in case your mental arithmetic is as bad as mine, this
is what Miles has to say about these formulae.
From the first formula, at Mach 1, ie M = 1, then M* also
is unity. That’s nice. Our red line on the graph is
the same for both M and M*. We can forget that. Consider it
done!
When M* is subsonic, P/Po will be less than 1 but never less
than 0.528
When M* is supersonic, P/Po can less than 0.528 but not greater,
When P/Po is really small, approaching zero, M* cannot exceed
6^.5
Wow, what rubbish: I cannot keep that in my head at all.
Lets put this in terms we can follow, we who love propellers.
If we have supersonic air rushing over the top of the airfoil
(green line), that is good, because it lowers the air pressure
on that surface and gives us lift. If it weren’t for
the spoil-sport high drag of the shockwave which comes with
the supersonic flow, we would be on a winner.
If we have subsonic air rushing over the lower surface (blue
line), then its pressure will always be greater than over
the top surface, and we again have good lift.
To finish. Remember that red line at Local Mach# 1? It was
near 0.5 on the P/Po axis. Well, from our formula, the value
was really 0.528! That number represents the dividing line
between 2 quote different flow behaviours of air: that between
subsonic and supersonic flow. Fascinating stuff, wouldn’t
you agree?
|