|
In my previous article, “Analytic
design of propellers - part 1”, I referred to the
need for a value of the lift coefficient Cl
derived from the Joukowski relationship; ie, Cl
derived from circulation theory. In my initial calculations
I tried equations given by Larrabee and Liebeck and Adkins.
These equations did not give realistic values when matched
to my known propeller performance data, so I was forced to
look further. The Larrabee paper was “Propeller Design
and Analysis for Modellers”, NFFS, 1979 (ref.1).
I found that Larrabees’ derivation was
riddled with “light loading” approximations, which
tended to remove the physics. Because I already know the performance
of my propellers, in particular the interference factors,
I am not hampered by some of Larrabees’ constraints.
Returning to Larrabees’ “Analytic
design of propellers having minimum induced loss”, NFFS
1977 (ref.2), I found Figure 2, p91, which is a sketch of
the motion of a helical vortex filament in the developed slipstream.
Ye Gods and little fishes, a what? Well, if
we think in terms of a single blade element, then the path
of that element influences an annulus of width say
r to r + dr, where
r is the radial station and dr
the width of the blade element. Inscribed on the surface of
the annulus we can imagine the helical path of the air displaced
by the blade element. This displaced air is part of the vortex
sheet shed by the entire propeller blade. Let us call this
the “helical vortex filament”.
The displaced air of the vortex filament has
velocity normal to the vortex sheet at station r
of value 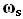 and with components axially of
and with components axially of 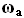 and radially of
and radially of 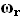 . .
Because we have only a finite number of blades,
which do not intersect all the air coming into the prop, we
need to invoke Prandtl’s vortex sheet spacing correction,
via the quantity F.
Then we may write, for a vortex filament at station r
to r + dr:
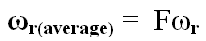
From the first term in equation (8)
(ref.1, p11), we can write:
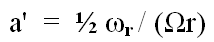
so that:
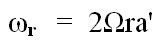
and
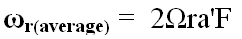
Moving to the first term in equation
(1) (ref.1, p10) yields:
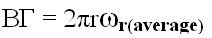
and substituting gives
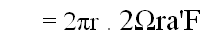
whence the circulation 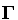 is is
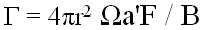
From equation (16) (ref.2,
p92), 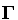 is also given by
is also given by
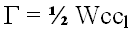
Equating the two expressions for 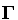 yields finally for the lift coefficient Cl
yields finally for the lift coefficient Cl
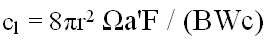
From the geometry of Larrabee’s Figure
4 (ref.2, p93) and the known performance of our propeller
we can get 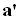 and
W
by varying the angle of attack and
W
by varying the angle of attack 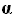 until Cl lies
on the lift slope curve at the design lift coefficient.
until Cl lies
on the lift slope curve at the design lift coefficient.
This completes the exercise, and hopefully yields
a value of Cl
which matches the empirical data.
In the above, B
is the number of blades, C the chord of the
blade element at radius r, W
the inflow vector after allowing for downwash, 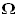 the angular velocity and
the angular velocity and 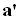 the torque plane interference factor.
the torque plane interference factor.
|